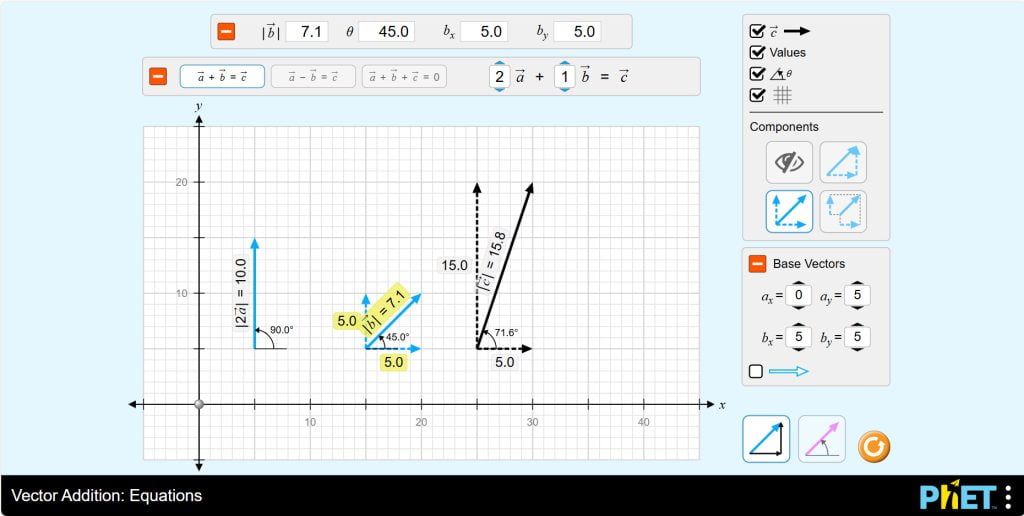
Meaning: share and balance
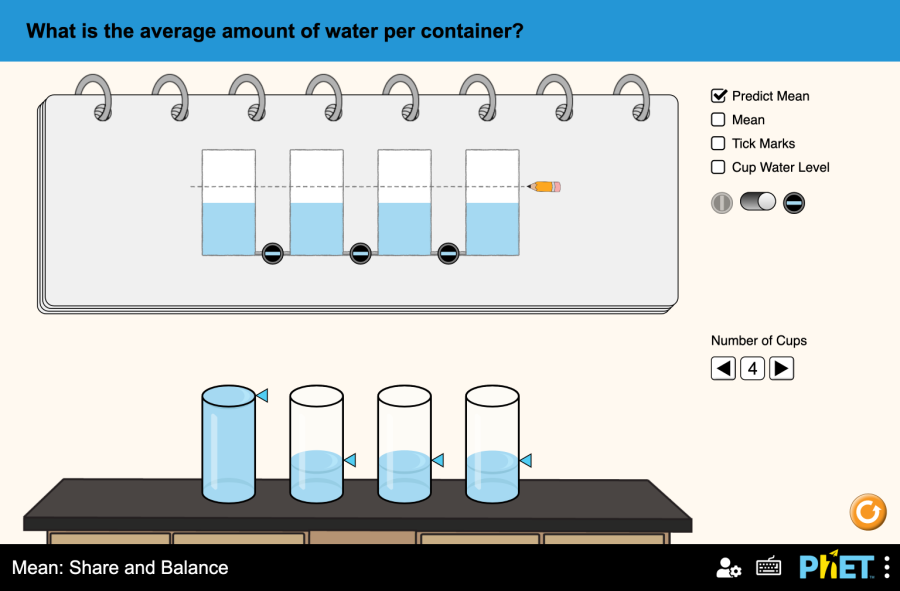
Mean: Share and Balance by PhET Interactive Simulations, University of Colorado Boulder, licensed under CC-BY-4.0 (https://phet.colorado.edu) Objective: This virtual activity is designed for use in geometry lessons on the following topic: Theoretical part Arithmetic mean The arithmetic mean is a number that shows the average of all the numbers in a group. To find the arithmetic mean, you need to add up all the numbers and divide the resulting sum by the number of those numbers. Formula: Average = (Sum of all values) / (Number of values) Example: Suppose we have a data set of 5 measurements of people’s height: 170 cm, 175 cm, 180 cm, 185 cm, 190 cm. Average: (170 + 175 + 180 + 185 + 185 + 190) / 5 = 180 cm. Virtual Experiment Modeling “mean fraction and equilibrium” allows students to understand mean in a variety of contexts. Students observe how gravity balances the height of water in two-dimensional beakers when the valves are opened. The flattened height is the average level of water in the beakers. Procedure: Step 1. Launch the simulation. In the workspace you will find Step 2. Activate the Predicted Average, Marks and Water Level buttons. Looking at the marks in the beaker, if it balances the water in the beaker, guess where the water level reaches the beaker by moving the knob there. Step 3. Press the middle button. Click “Restore Balance”. Compare the actual average water level with the estimated average water level. Step 4. Press the “Restart” button. Increase the number of jars as desired. Step 5. Repeat the process for 2 cups. Step 6. Experiment by changing the number of cups to your liking. Conclusion Students were introduced to the concept of average through this virtual activity. They performed different manipulations of different levels of water in a beaker and balanced the water.
Meaning: share and balance Read More »