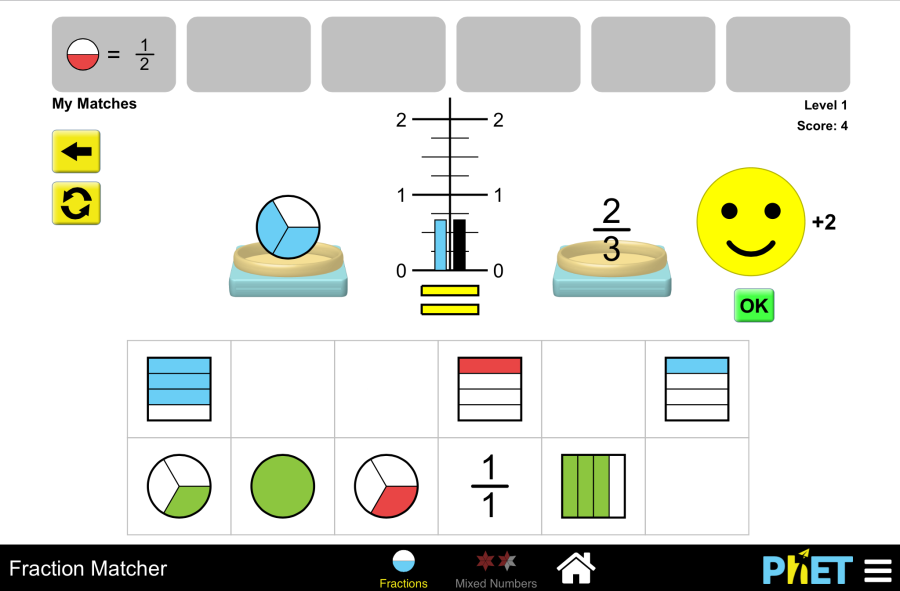
Fraction Matcher
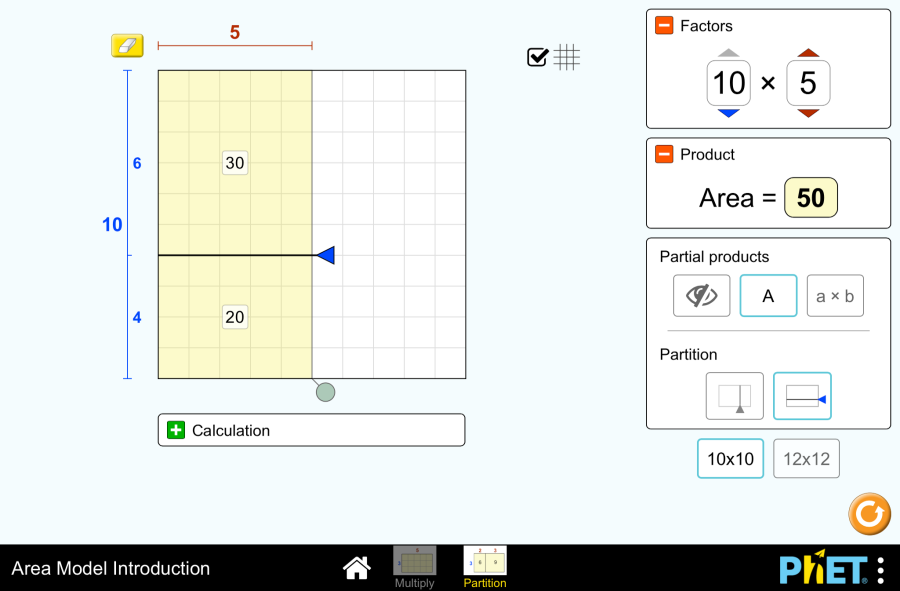
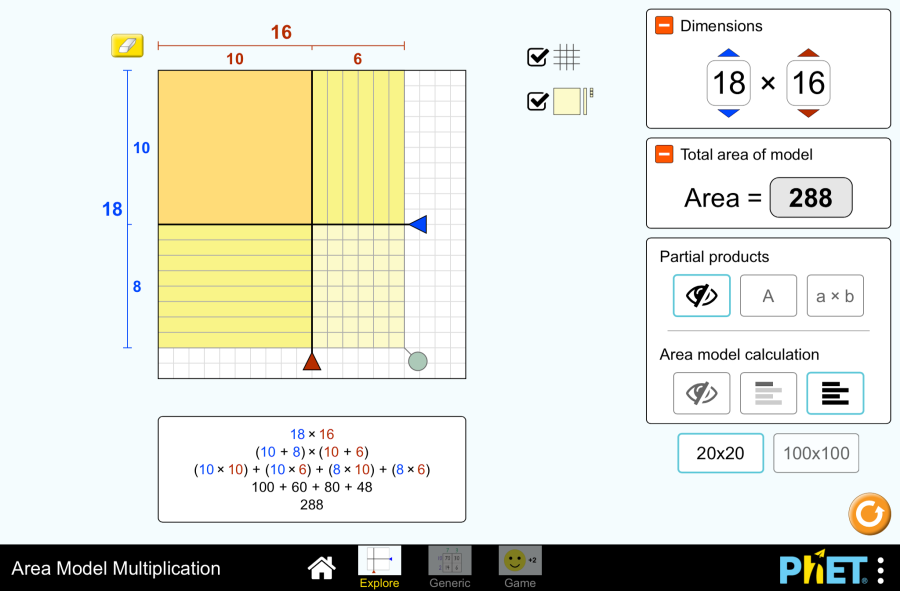
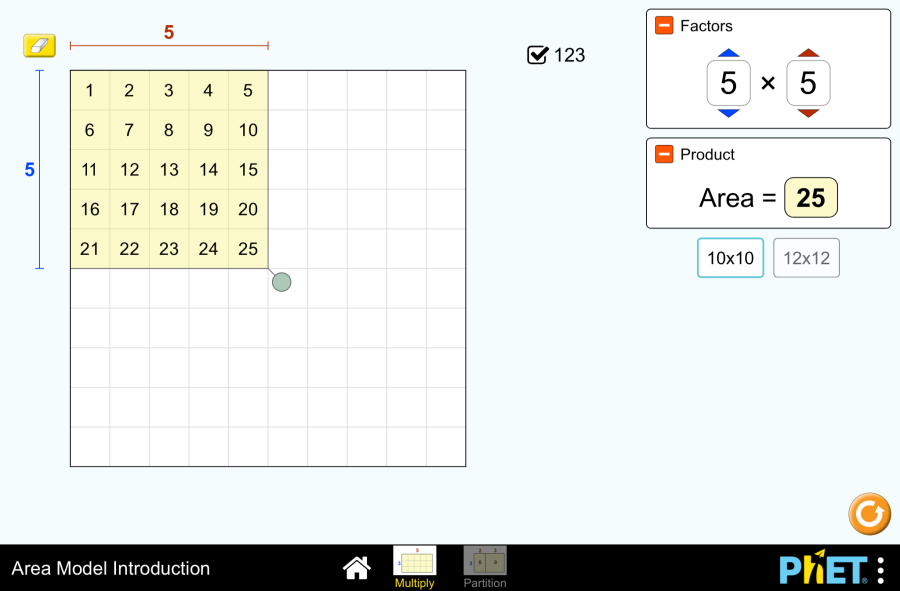
Fraction Matcher by PhET Interactive Simulations, University of Colorado Boulder, licensed under CC-BY-4.0 (https://phet.colorado.edu) Objective: This virtual activity is designed for use in mathematics lessons on the following topics Theoretical part Ordinary fractions are numbers represented as fractions where the numerator and denominator are integers and the denominator is not zero. Writing a fraction: Example: Meaning of the fraction: Example: Types of fractions: Example of a mixed number: Writing a mixed number: Converting fractions to mixed numbers: Virtual experiment “Fraction Matcher” virtual activity teaches students to find and match matching fractions using numbers and pictures. Performs fraction calculations in a fun way to easily master the topic of simple fractions. Match the same fractions using different numbers and fraction representations. Course of work: Section 1: Play with correct and incorrect simple fractions Step 1. Start the simulation: You will be presented with 2 different modes: “Fraction” and “Mixed Numbers”. Open the “Fraction” section. Step 2. In the work area you will be presented with 8 different levels of problems. Levels 1-2 use only fractions smaller than 1. Levels 3-6 use fractions smaller than 2. Levels 7-8 use only fractions greater than 1 and less than 2. Step 3. Open the first level. In the work area, you will see Step 4. Bring any fraction to the scales by left-clicking and dragging it. Step 5. Among the remaining fractions, find a fraction that is equal or proportional to the fraction on the scale. Place it on the second weight. Step 6. Check for correctness by clicking on the “Check” button. If the fractions are equal, click “OK” and perform the next alignment. If there is an error, click “Try Again” and compare the fractions from the beginning. Step 7. Complete the tasks in a level and move on to the next level. Section 2: Mixed Numbers Game Step 8. Open the “Mixed Numbers” Section. In the workspace, you will see 8 different levels of problems. Levels 1-6 use less than 2 mixed number fractions. Levels 7-8 use more than 1 and less than 2 fractions. Step 9. Open the first level. This section also introduces the work area as in the first section. Here you will do problems with mixed numbers. Step 10. Move any fraction to the scales by left-clicking and dragging. From the remaining fractions, find one that is equal to or proportional to the fraction on the scale. Place it on the second scale. Step 11. Check your work by clicking on the “Check” button. Step 12. Complete the tasks of one level and move on to the next levels. Conclusion In this simulation, students worked on fraction-related game tasks to further explore the topic of fractions. They used the basic property of fractions to reduce fractions, compare fractions, and make fractions equal to each other.